7796. Кафе
Сегодня в кафе Нового Университета
(НУ) пришли n студентов. Каждый из
них хочет выпить чашку кофе и съесть одно пирожное (никто из них не согласен
только на кофе либо только на пирожное – в этом случае студент уходит). В кафе
подают m видов кофе и k видов пирожных. Для каждого из видов
кофе или пирожного известно, сколько чашек или порций этого вида имеется в
наличии.
Кроме того, у каждого студента есть
свои вкусовые предпочтения. Для каждого студента известно, какие виды кофе и
пирожных он любит. Никто из студентов не согласен есть или пить то, что ему не
нравится.
Хозяин кафе задумался: какое
максимальное количество студентов он сможет обслужить? А Вы можете посчитать
это число?
Вход. Первая
строка содержит целые числа n, m, k
(1 ≤ n, m, k ≤ 500).
Во второй
строке записано m целых чисел через
пробел C1, C2, ..., Cm
(1 ≤ Ci ≤ 500)
– количество чашек кофе каждого вида, имеющихся в наличии.
В третьей
строке записано k целых чисел через
пробел P1, P2, ..., Pk
(1 ≤ Pi ≤ 500)
– количество порций пирожных каждого вида, имеющихся в наличии.
В
следующих n строках дана информация о
том, какие виды кофе любит каждый студент. i-я
строка (1 ≤ i ≤ n) содержит число Xi, за которым следуют различные числа A1, A2,
..., AXi – виды кофе,
которые любит i-й студент.
Следующие n строк задают информацию о том, какие
виды пирожных любит каждый студент. i-я
строка (1 ≤ i ≤ n) содержит число Yi, за которым следуют различные числа B1, B2,
..., BYi – виды пирожных, которые
любит i-й студент.
Выход. Выведите
единственное число, ответ на задачу.
|
Пример входа |
Пример выхода |
|
2 3 1 5 1 3 2 3 1 2 3 1 2 1 1 1 1 |
2 |
РЕШЕНИЕ
максимальный поток
Анализ алгоритма
Построим
граф на списках смежности (для избежания Time Limit), имеющий один исток и один
сток. Синие вершины представляют виды кофе, серые – виды пирожных. Желтыми
будем обозначать студентов. Студентов раздвоим чтобы каждый из них смог
получить не более одного кофе и пирожного.
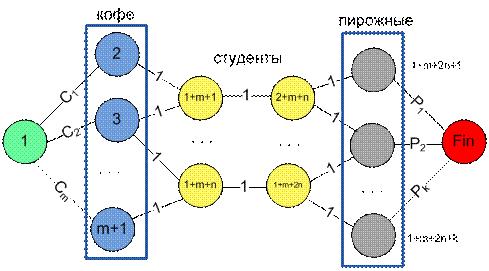
Максимальный
поток равен максимальному
количеству студентов, которое сможет обслужить хозяин кафе.
Пример
Построим
граф из примера. Вершина 1 является истоком, вершина 10 стоком.
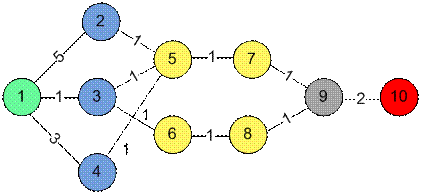
Максимальный
поток равен 2.
Реализация алгоритма
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#define MAX 2100
#define INF 0x3F3F3F3F
using namespace
std;
class Edge
{
public:
int vTo;
long long Cap, Flow;
Edge(int vTo, long long Cap, long long Flow)
: vTo(vTo),
Cap(Cap), Flow(Flow) {}
};
class Graph
{
public:
int n;
vector<vector<int>
> g;
// ребра графа =
числа-указатели на реальные ребра в AllEdges
vector<Edge>
AllEdges; // Реальные ребра графа
vector<int> ptr, d;
Graph(int n = 1) : n(n)
{
g.assign(n+1,vector<int>());
}
void AddNotOrientedEdge(int
From, int To, int
Len)
{
Edge e1 =
Edge(To,Len,0);
g[From].push_back(AllEdges.size());
AllEdges.push_back(e1);
Edge e2 =
Edge(From,0,0);
g[To].push_back(AllEdges.size());
AllEdges.push_back(e2);
}
long long bfs(int s)
{
int qHead = 0, qTail = 0;
int *q = new int[n+1];
q[qTail++] = s;
d.assign(n+1,-1);
d[s] = 0;
while (qHead < qTail)
{
int v = q[qHead++];
for (int i = 0; i
< g[v].size(); i++)
{
Edge e =
AllEdges[g[v][i]];
int to = e.vTo;
if ((d[to] ==
-1) && (e.Flow < e.Cap))
{
q[qTail++] =
to;
d[to] = d[v]
+ 1;
}
}
}
delete[] q;
return d[n] != -1;
}
long long dfs(int v, long long flow)
{
if (!flow) return 0;
if (v == n) return flow;
for (int &i =
ptr[v]; flow && (i < (int)g[v].size());
i++)
{
int EdgeId = g[v][i];
Edge e =
AllEdges[EdgeId];
int to = e.vTo;
if (d[to] != d[v] + 1) continue;
long long pushed =
dfs(to, min(flow, e.Cap - e.Flow));
if (pushed)
{
AllEdges[EdgeId].Flow += pushed;
AllEdges[EdgeId
^ 1].Flow -= pushed;
return pushed;
}
}
return 0;
}
long long Dinic(int Start)
{
long long flow = 0;
for (;;)
{
if (!bfs(Start)) break;
ptr.assign(n+1,0);
while (long long pushed = dfs(Start, INF))
flow += pushed;
}
return flow;
}
};
Graph *g;
int cnt, i, j, k, m, n, c, x, Final,
MaxFlow;
int main(void)
{
scanf("%d %d %d",&n,&m,&k);
Final = 1 + m + 2*n +
k + 1;
g = new Graph(Final);
for(i = 2; i <= 1 + m; i++)
{
scanf("%d",&c);
g->AddNotOrientedEdge(1,i,c);
}
for(i = 1 + m + 2*n + 1; i <= 1 + m + 2*n + k;
i++)
{
scanf("%d",&c);
g->AddNotOrientedEdge(i,Final,c);
}
for(i = 1; i <= n; i++)
{
scanf("%d",&cnt);
for(j = 1; j <= cnt; j++)
{
scanf("%d",&x);
g->AddNotOrientedEdge(x+1,1+m+i,1);
}
}
for(i = 1; i <= n; i++)
{
g->AddNotOrientedEdge(1+m+i,1+m+n+i,1);
}
for(i = 1; i <= n; i++)
{
scanf("%d",&cnt);
for(j = 1; j <= cnt; j++)
{
scanf("%d",&x);
g->AddNotOrientedEdge(1+m+n+i,1+m+2*n+x,1);
}
}
MaxFlow =
g->Dinic(1);
printf("%d\n",MaxFlow);
return 0;
}